Multicategorical Skill Scores
While some statistics for multicategorical forecasts require simplifying the contingency table to two-categories, and therefore only show the forecast’s quality in respect to the individual category, certain skill scores are designed to evaluate forecasts with multiple categories, allowing the skill score to reflect the quality of the entire forecast spectrum.
Heidke Skill Score (HSS)
HSS has a general form to accommodate multicategory forecasts. While more computationally intense than the two-category equation provided, the multi-category formulation is also based on comparison of the percent correct in the forecast relative to the proportion correct that would be achieved by a “random” forecast. The relative comparison is often with sources other than a “random” forecast, including older versions of a model and climatology. This general form is
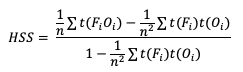
Note that t(FiOi) is the number of forecasts in category i of the multicategory contingency table that had an observation of Oi, t(Fi) is the total number of forecasts in category i, and n is the total number of occurrences and non-occurrences.
Hanssen-Kuipers Discriminant (HK)
Similarly, HK is generalized to
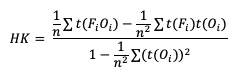
Gerrity Skill Score
The Gerrity Skill Score is designed specifically for multicategory forecasts. While it is not as easily calculated as HSS and HK, it is useful for demonstrating the ability of the forecasts to delineate the correct event category when compared to random chance. The Gerrity Skill Score properly penalizes a forecast that has more than two options for an event, something not captured in the generalized forms of HSS or HK. This is achieved through the use of weights, sj,j, which correspond to correct forecasts, and sj,i, which represent weights for incorrect forecasts. These weights are given as
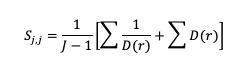
and
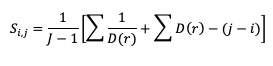
where D(r) is the likelihood ratio using dummy summation index r, calculated using
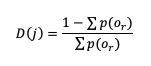
where p(or) is the probability of a sample climatology.
Finally, the Gerrity Skill Score is computed through summing the product of the scoring weights and their corresponding joint probability distribution. That distribution is found by taking each count of the contingency table cell and dividing it by the total number of occurrences and non-occurrences across all cells, n. See how to use these statistics in METplus!