Verification Statistics for Continuous Forecasts

The nature of continuous forecast verification is a direct comparison of the forecast and observed values and measurement of the relationship of those two values over the real number range. We can easily infer that the scalar statistics and skill scores used for these kinds of forecasts will be different from those used for binary and multi-categorical forecasts. In fact many of the statistics that are used as “introductory statistics” are derived for continuous verification along the real number range, as continuous verification is a natural way we look at forecasts (i.e., how close or far the forecast and observed values are from each other).

Mean Errors

The simplest continuous measure is the mean error (ME), which is the average difference between two groups of data. So when you see “error” it is simply a measure of a difference. ME is calculated as

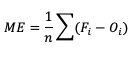
ME can range over the real numbers and has the obvious advantage of providing immediate insight into how far away, on average, the forecast values are from their corresponding observations. It is extremely easy to calculate, with a perfect forecast (i.e., a forecast that exactly corresponds to the observations) characterized by an ME of 0. ME serves as an important measurement of arithmetic bias. As a measure of bias,  ME does not include a method for compensating for the magnitude of the differences between the forecast-observation pairs, and a forecast that has compensating errors could receive a mean error of 0. Essentially, ME provides an indication of whether a forecast has errors that - on average - are centered on zero; or if it is overforecasting or underforecasting on average. Consider the following scenario for wind speed forecasts at the same location for four different times: 

You’ll find the ME computed with these data equals 0, even though the difference between forecast and observation values for all of the times are non-zero. That’s because those errors that are positive (the forecast was greater than the observed value) are exactly negated by those errors that are negative (the forecast was less than the observed value). As noted earlier, ME is a good measure of bias; however, it is not a measure of accuracy.

This ability to effectively “hide” errors calls for a more robust error calculation to understand the forecasts’ accuracy. To that end, a few additional choices for measuring error are available.

Mean absolute error (MAE), while similar to ME, examines the absolute values of the errors, which are summed and averaged, providing a measure of accuracy as opposed to bias. Examining the absolute values of the errors restricts MAE’s range from zero to positive infinity, with a perfect score of zero:

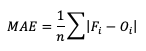
MAE also differs from ME in that it measures forecast accuracy, while ME measures bias. MAE provides a summary of the average magnitudes of the errors, but does not provide information about the direction (positive or negative) of the error magnitude.

Mean Squared Error (MSE) is another statistic focused on the characteristics of the forecast errors that measures forecast accuracy. In particular, MSE summarizes the squared differences between the forecast and observed values:

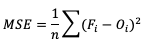
This measure has the same limits and perfect score as MAE, but squaring the differences does more than remove the sign of the differences: by squaring the error values, differences greater than one are penalized more severely than those that are less than one, with the penalty increasing at a squared rate. Using MSE, a forecast that over-forecasts temperature by two degrees from the observed value consistently over six time steps will have a smaller MSE than a forecast that over-forecasts temperature from the observed value by three degrees for three time steps and matched the observed value for the remaining three time steps.

The final error statistic to discuss is Root Mean Squared Error (RMSE). One of the most familiar statistical measures, RMSE is simply the square root of MSE, and has the same units as the forecasts and observations, providing an average error with a square-weight:

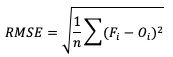
Similar to MSE, RMSE penalizes larger error magnitudes than smaller ones, and like MSE, RMSE provides no information on the sign (positive or negative) of the errors. It has the same range of values as MSE and a perfect forecast score would be an RMSE of zero. See how to use these statistics in METplus!

Standard Deviations

Unlike the family of mean error statistics, standard deviation focuses more on the individual groups of value sources; namely, the forecasts and observations. Standard deviations are a measure of how the variability of the values in a dataset differs from the average of their respective group. So keep in mind the general equation provided below can be applied to both observations and forecasts (and in some cases it may be meaningful to compare the standard deviation of the forecasts to the standard deviation of the observations):

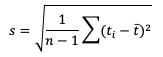
See how to use this statistic in METplus!

Multiplicative Bias

Like some of the other verification statistics for continuous forecasts, multiplicative bias (MBIAS) measures the ratio of the average forecast to the average observation. MBIAS is the ratio between these two averages, calculated using the following formula and has a range of all real numbers:

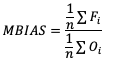
MBIAS has some of the same drawbacks as ME. In particular, MBIAS does not indicate the magnitudes of the forecast errors, which allows a perfect score of 1 to be achieved if the forecast errors compensate for each other (see the example for ME above for more information). It is recommended that any variable fields that utilize MBIAS contain all the same value signs (e.g. positive or negative) as mixing value signs together (for example, temperatures) would result in strange or unusable MBIAS results that included even more value compensation. See how to use this statistic in METplus!

Correlation Coefficients (Pearson, Spearman Rank, and Kendall’s Tau)

Because continuous forecasts and observations exist on the same real value spectrum, measurements of the linear association of the forecast-observation pairs create a vital foundation for verification statistics. Three measures of correlation (Pearson, Spearman Rank, and Kendall's Tau) measure this relationship in different ways.

Beginning with Pearson correlation coefficient, PR_CORR, the linear association of the forecast-observation pairs is measured using a sample covariance (e.g. the summed squared anomalies of two groups) and dividing by the product of the same two group’s standard deviations. In forecast verification, these two groups are the forecast and observation datasets and appear as

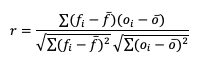
with r as the typical notation for the PR_CORR outside of METplus. From a visual perspective, PR_CORR measures the closeness of pairs of points, (i.e., representing the forecast and corresponding observation values) corresponding to a diagonal line. More generally these scatter plots can suggest the apparent relationship of any two variable fields, but for the purpose of this tutorial we will stay focused on the forecast-observation comparison. PR_CORR can range from negative one to positive one with either extreme of the range representing a perfect positive or negative linear association between the forecasts and observations. The PR_CORR remains sensitive to outliers and can produce a good correlation value for a poor forecast if that forecast has compensative errors.

Another way to estimate the linear association between forecasts and their corresponding observations involves ranking the forecast values when compared to the forecast group’s total range, do the same for the observation group, and then compute the correlation values. Spearman Rank correlation coefficient (SP_CORR) takes this approach while utilizing the same equation as PR_CORR. Because the rank values of both the forecast and observation datasets used to calculate SP_CORR are restricted to the integer values of 1 to n (the total number of matched forecast-observation pairs), the equation of SP_CORR can be simplified to

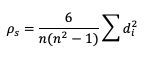
where di denotes the difference in ranking between the pair of datafields.

What does ranking  of matched pairs look like with actual data? Let’s use the following scenario of rainfall forecasts and the observed rainfall over a five hour period for a set location:

 Using a ranking system for the datasets where 0.0” is assigned 1 and everything greater than that value is assigned a value that is integer-based, monotonically increasing by 1, the data table above would be transformed into the following ranks:

It is important that the forecast-observation pairs stay paired together, even when transformed into their rank values. Note the case when there is a tie in the ranks (i.e. a value appears more than once), all of the values receive the same average rank, keeping the total average rank for the number of values (in this scenario, five) consistent with the SP_CORR equation assumption. The next step is calculating the differences between the forecast ranks and the observed ranks, squaring the differences and summing them. After that, apply the rest of the equation and you should find ρ_s =0.825, a strong correlation value.

The Kendall’s Tau statistic (𝝉) is a variation on the SP_CORR equation ranking method. While all of the variable field values are ranked as was the case with SP_CORR, it’s the relationship between a pair of ranks and the pairs of ranks that follow, rather than the ranks within a given pair, that constitute 𝝉. To better understand, let’s first look at the equation for 𝝉:

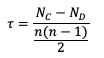
In the equation, N_C is a count of the concordant pairs, and N_D is a count of the discordant pairs. Simply put, a concordant pair is when a reference pair has rank values that are both larger or both smaller than a comparison pair. For example, consider the two pairs (3, 5) and (6, 8). Regardless of which pair is treated as the reference pair, the comparison pair will have both of the larger rank values (the case where (3, 5) is the reference pair) or both of the smaller rank values (the case where (6, 8) is the reference pair). A concordant pair is the complement to this: each pair in the comparison has one value that is bigger and one that is smaller. In the case of (3, 5) and (6, 2) the comparisons are considered discordant. In the case where the compared pairs are identical, there are multiple methods to choose: N_C and N_D can be incremented by ½ each, the tie can be ignored, or the tie can be penalized. For simplicity in counting, it is recommended to arrange one of the datasets in ascending or descending order (being careful to keep the matched pairs together) so that fewer comparisons need to be made.

To show how 𝝉 is calculated, let’s return to the previous example used to calculate SP_CORR. Because we’re using the same rainfall values, the rankings of those values will also be the same. For the simplicity of counting concordant and discordant pairs, the forecast ranks have been arranged in increasing order (which explains why Hour 5 is now proceeding Hour 1):

From this small change in the ordering, we see that two of the observed ranks do not increase (going from left to right): between Hour 5 and Hour 1 (they match at 1.5), and between Hour 3 and Hour 4 (5 compared to 4). Additionally, the forecast ranks between Hour 1 and Hour 2 do not increase (they match). In order to account for these ties, a “penalty” will be calculated using the following equation:

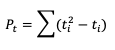
Where ti is the number of ranks that are involved in a given tie.  Because both the forecast and observed ranks have a tie of two ranks, both will receive a Pt penalty of 2. As a result of this new handling of ties, an alternate form of 𝝉 sometimes referred to as 𝝉b must be used:

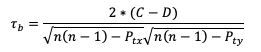
Using this slightly modified equation, we find a 𝝉b value of 0.56. As 𝝉 has the same range as SP_CORR (-1 to 1), a value of 0.56 shows some positive correlation between the two datasets. See how to use these statistics in METplus!

Anomaly Correlation

While similar to the traditional correlation coefficient, anomaly correlation is a somewhat different formulation: rather than directly comparing the pairs of forecast and observation values relative to the respective group averages, as is the case in PR_CORR, anomaly correlation is a measure of the deviations of forecast and observation values from climatological averages. Utilizing this third independent dataset for comparisons highlights any pattern of departures from the climatology, a correspondence of the forecast anomalies to the observed anomalies.

There are two widely used versions of anomaly correlation. The first is the centered anomaly correlation, which includes the mean error relative to the climatology. This version is calculated using

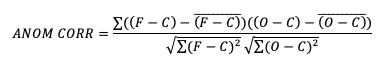
If it is not desirable to include the errors, the uncentered anomaly correlation is the better choice:

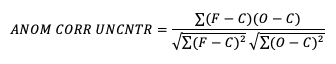
While there is an added effort required to find the matching climatology reference dataset for this statistic, it remains a highly resourceful statistic to use, especially with spatial verification, and is commonly used in operational forecasting centers. Anomaly correlation has a range from -1 to 1. See how to use this statistic in METplus!

METplus Solutions for Continuous Forecast Verification

Now that you know a bit more about continuous, deterministic forecasts and the related statistics, it’s time to show how you can access those same statistics in METplus!

Unsurprisingly METplus requires a slightly different approach to continuous variables and the thresholds that are used on these datasets. Rather than the cat_thresh arrays that are used for categorical variable fields, METplus uses cnt_thresh for filtering data prior to computing continuous statistics. Keep that in mind if you end up with a blank continuous line type file output; you may have not applied the correct thresholds!

In order to better understand the delineation between METplus, MET, and METplus wrappers which are used frequently throughout this tutorial but are NOT interchangeable, the following definitions are provided for clarity:

• METplus is best visualized as an overarching framework with individual components. It encapsulates all of the repositories: MET, METplus wrappers, METdataio, METcalcpy, and METplotpy.
• MET serves as the core statistical component that ingests the provided fields and commands to compute user-requested statistics and diagnostics.
• METplus wrappers is a suite of Python wrappers that provide low-level automation of MET tools and plotting capability. While there are examples of calling METplus wrappers without any underlying MET usage, these are the exception rather than the rule

MET Solutions 

The MET User’s Guide provides an Appendix that dives into each and every statistical measure that it calculates, as well as the line type it is a part of. Statistics are grouped together by application and type and are available to METplus users in line types. For example, many of the statistics that were discussed above can be found in the Continuous Statistics (CNT) line type, which logically groups together statistics based on continuous variable fields.

For MET, which line types are output depends on your selection of the appropriate line type using the output_flag dictionary. Note that certain line types may or may not be available in every tool: for example, both Point-Stat and Grid-Stat produce CNT line types, which allows users access to the various continuous statistics for both point-based observations and gridded observations. But Ensemble-Stat is the only tool that can generate a Ranked Probability Score (RPS) line type which contains statistics relevant to the analysis of ensemble forecasts. If you don’t see your desired statistic in the line type or tool you’d expect it to be in, be sure to check the Appendix to see if the statistic is available in MET and which line type it’s currently grouped with.

As for the previous statistics that were discussed, here’s a link to the User’s Guide Appendix entry that discusses its use in MET:

• ME
• MAE
• MSE
• RMSE
• S (note that the linked s is for forecast; the observation s2 is just below it)
• MBIAS
• PR_CORR
• SP_CORR
• 𝝉 or KT_CORR
• ANOM_CORR

METplus Wrapper Solutions

The same statistics that are available in MET are also available with the METplus wrappers. To better understand how MET configuration options for statistics translate to METplus wrapper configuration options, you can utilize the Statistics and Diagnostics Section of the METplus wrappers User’s Guide, which lists all of the available statistics through the wrappers, including what tools can output what statistics. To access the line type through the tool, find your desired tool in the list of available commands for that tool. Once you do, you’ll see the tool will have several options that contain _OUTPUT_FLAG_. These will exhibit the same behavior and accept the same settings as the line types in MET’s output_flag dictionary, so be sure to review the available settings to get the line type output you want.

The following two examples show a generalized method for calculating continuous statistics: one for a MET-only usage, and the same example but utilizing METplus wrappers. These examples are not meant to be completely reproducible by a user: no input data is provided, commands to run the various tools are not given, etc. Instead, they serve as a general guide of one possible setup among many that produce continuous statistics.

If you are interested in reproducible, step-by-step examples of running the various tools of METplus, you are strongly encouraged to review the METplus online tutorial that follows this statistical tutorial, where data is made available to reproduce the guided examples.

In order to better understand the delineation between METplus, MET, and METplus wrappers which are used frequently throughout this tutorial but are NOT interchangeable, the following definitions are provided for clarity:

• METplus is best visualized as an overarching framework with individual components. It encapsulates all of the repositories: MET, METplus wrappers, METdataio, METcalcpy, and METplotpy.
• MET serves as the core statistical component that ingests the provided fields and commands to compute user-requested statistics and diagnostics.
• METplus wrappers is a suite of Python wrappers that provide low-level automation of MET tools and plotting capability. While there are examples of calling METplus wrappers without any underlying MET usage, these are the exception rather than the rule.

MET Example of Continuous Forecast Verification

Here is an example that demonstrates deterministic forecast verification in MET.

For this example, let’s examine two tools, PCP-Combine and Grid-Stat. Assume we wanted to verify a 6 hour period of precipitation forecasts over the continental United States. Using these tools, we will first combine the forecast files, which are hourly forecasts, into a 6 hour summation file with PCP-Combine. Then we will use Grid-Stat to place both datasets on the same verification grid and let MET calculate the continuous statistics available in the CNT line type. Starting with PCP-Combine, we need to understand what the desired output is first to know how to properly run the tool from the command line, as PCP-Combine does not use a configuration file. As stated previously, this scenario assumes the precipitation forecasts are hourly files and need to match the 6 hour observation file time summation. Of the four commands available in PCP-Combine, two seem to provide potential paths forward: sum and add.

While there are multiple methods that may work to successfully summarize the forecast files from these two commands, let’s assume that our forecast data files contain a time reference variable that is not CF-compliant {link to CF compliant time table in MET UG here}. As such, MET will be unable to determine the initialization and valid time of the files (without being explicitly set in the field array). Because the “add” command only relies on a list of files passed by the user to determine what is being summed, that is the command we will use.

With the information above, we construct the command line argument for PCP-Combine to be:

The command above displays the required arguments for PCP-Combine’s “add” command as well as an optional argument. When using the “add” command it is required to pass a list of the input files to be processed. In this instance we used a list of files, but had the option to pass an ASCII file that contained all of the files instead. Because each of the input forecast files contain the exact same variable fields, we utilize the “-field” argument to list exactly one variable field to be processed in all files. Alternatively we could have listed the same field information (i.e. 'name="P01M_NONE"; level="(0,*,*)";') after each input file. Finally, the output file name is set to “hrefmean_2017051006_A06.nc”, which contains references to the valid time of the file contents as well as how many hours the precipitation is accumulated over. The optional argument “-name” sets the output variable field name to “APCP_06”, following GRIB standard practices.

After a successful run of PCP-Combine we now have a six hour accumulation field forecast of precipitation and are ready to set our Grid-Stat configuration file. Starting with the general Grid-Stat configuration file {provide link here}, the following would resemble minimum necessary settings/changes for the fcst and obs dictionaries:

Both input files are netCDF format and so require the asterisk and parentheses method of level access. The observation input file level required a third dimension as more than one observation time is available. We used the “@” symbol to take advantage of MET’s ability to parse time dimensions by the user-desired time, which in this case was the verification time. Note how the variable field name that was set in PCP-Combine’s output file is used in the forecast field information. Because the two variable fields are not on the same grid, an independent grid is chosen as the verification grid. This is set using the in-tool method for regridding:

Now that the verification is being performed on our desired grid and the variable fields are set to be read in, all that’s left in the configuration file is to set the output. This time, we’re interested in the CNT line type and set the output flag library accordingly:

And as a sanity check we can see the input fields the way MET is ingesting them by selecting the desired nc_pairs_flag library settings:

All that’s left is to run MET with a command line prompt:

The resulting two files have a wealth of information and statistics. The netCDF output contains our visual confirmation that the forecast and observation input fields were interpreted correctly by MET, as well as the difference between the two fields which is provided below:

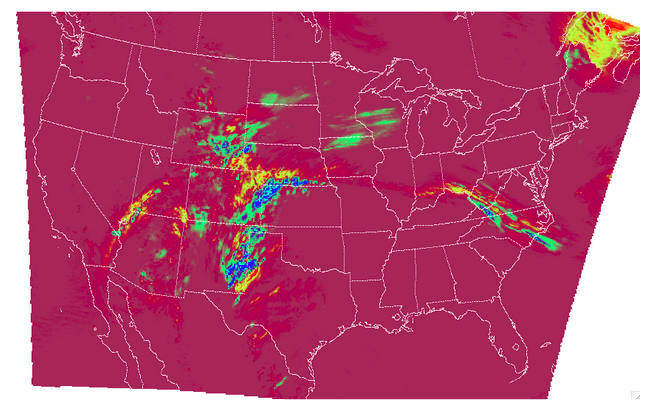
 For the CNT line type output we review the .stat file and find something similar to the following:

The columns that are available in the CNT line type are listed in the MET User’s Guide guidance for CNT line type {provide link here}. After the declaration of the line type (CNT), the familiar TOTAL or matched pairs column, we find a wealth of statistics including the forecast and observation means, the forecast and observation standard deviations, ME, MSE, along with all of the other statistics discussed in this section, all with their appropriate lower and upper confidence intervals and the bootstrap confidence intervals. Note that because the bootstrap library’s n_rep variable was kept at its default value of 0, bootstrap methods were not used and appear as NA in the stat file. You’ll also note that the ranking statistics (SP_CORR and KT_CORR) are listed as NA because we did not set rank_corr_flag to TRUE in the Grid-Stat configuration file. This was done intentionally; in order to calculate ranking statistics MET needs to assign each and every matched pair a rank and then perform the calculations. With a large dataset with numerous matched pairs this can significantly increase runtime and be computationally intensive. Given our example had over 1.5 million matched pairs, these statistics are best left to a smaller domain. Let’s create that smaller domain in a METplus wrappers example!

METplus Wrapper Example of Continuous Forecast Verification

To achieve the same success as the previous example but utilizing METplus wrappers instead of MET, very few adjustments would need to be made. Because METplus wrappers have the helpful feature of chaining multiple tools together, we’ll start off by listing all of the tools we want to use. Recall that for this example, we want to include a smaller verification area to enable the rank correlation statistics as well. This results in the following process list:

The second listing of GridStat uses the instance feature to allow a second run of Grid-Stat with different settings. Now we need to set the _VAR1 settings appropriately:

We’ve utilized a different setting, FCST_PCP_COMBINE_OUTPUT_NAME, to control what forecast variable name is verified. This way if a different forecast variable were to be used in a later run (assuming it had the same level dimensions as the precipitation), the forecast variable name would only need to be changed in one place instead of multiple. We also utilize METplus wrappers' ability to set an index based on a time, behaving similarly to the “@” usage in the MET example. Now we need to create all of the settings for PCPCombine:

From these settings, we see that all of the arguments from the command line for PCP-Combine are present: we will use the “add” method to loop over six netCDF files, each containing a variable field name of P01M_NONE and accumulation times of one hour. The output variable should be named APCP_06 and will be stored in the location as directed by FCST_PCP_COMBINE_OUTPUT_DIR and FCST_PCP_COMBINE_OUTPUT_TEMPLATE (not shown above).

Because the loop/timing information is controlled inside the configuration file for METplus wrappers (as opposed to MET’s non-looping option), that information must also be set accordingly, paying close attention that both instances of GridStat and PCPCombine will behave as expected:

Recall that we need to perform the verification on an alternate grid for one of the instances, and a small subset of the larger area in the other. So in the first instance configuration file area (anywhere outside of the [rank] instance configuration file area) we add

And set the [rank] instance up as follows:

For this instance of GridStat, we’ve set our own verification area using the grid definition option {link grid project here}, and utilized the OVERRIDES option {link to the OVERRIDES discussion here} to set the rank_corr_flag option, which is currently not a METplus wrapper option, to TRUE. Because both GridStat instances will create CNT output, the [rank] instance CNT output would normally overwrite the first GridStat instance. To avoid this, we create a new output template for the [rank] instance of GridStat to follow, preserving both files.

Finally, the desired line types and nc_pairs_flag settings need to be selected for output. This can be done outside of the [rank] instance, as any setting that is not overwritten by an instance further down the configuration file will be propagated to all applicable tools in the configuration file:

With a proper setting of the input and output directories, file templates, and a successful run of METplus, the same .stat output and netCDF file that were created in the MET example would be produced here, complete with CNT line type. However this example would result in two additional files: one .stat file that contains values for the rank correlation statistics and a netCDF file with the smaller area that was used to calculate them. The contents of that second .stat file would look something like the following:

We can see the smaller verification area resulted in only 1,600 matched pairs, which is much more reasonable for rank computations. SP_CORR was 0.41127 showing a positive correlation, while KT_CORR was 0.28929, a slightly weaker positive correlation. METplus goes the additional step and also shows that of the 1,600 ranks that were used to calculate KT_CORR, it found 1,043 forecast ranks that were tied and 537 observation ranks that were tied. Not something that would be easily computed without the help of METplus!