Verification Statistics for Binary Categorical Forecasts

Most meteorological forecasts would be described as non-probabilistic, meaning the forecast value given is provided with no additional information of certainty in that value. Another term for this type of forecast is deterministic and will be the focus of the verification statistics in this section. For more information on probabilistic forecasts and their corresponding statistics please refer to the probabilistic section. When verifying binary categorical forecasts, the only important factor is whether or not the event occurred: the assumed certainty in the forecast is 100%.

Numerous computationally-easy (and very popular) scalar statistics are within reach without too much manipulation of a contingency table’s counts.

Accuracy (Acc)

The scalar attribute of Accuracy is measured as a simple ratio between the forecasts that correctly predicted the event and the total number of occurrences and non-occurrences, n. In equation format,

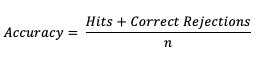
This measure (often called “Percent Correct”) is very easily computed and addresses how often a forecast is correctly predicting an event and non-event. As most verification resources will warn you, however, this measure should be used with caution, especially for an event that happens only rarely. The Finley tornado forecast study (1884) is an excellent example of the need for caution, with Finley reporting a 96.6% Accuracy for predicting a tornado due to the overwhelming count of correct negatives. Peers were quick to point out that a higher Accuracy (98.2%) could have been achieved with a persistence forecast of No Tornado! See how to use this statistic in METplus!

Probability of Detection (POD)

Probability of Detection (POD), also referred to as the Hit Rate, measures the frequency that the forecasts were correct given that the forecast predicts an occurrence. Rather than computing the ratio of the correct forecasts to the entire occurrence and non-occurrence count (i.e., as in Accuracy), POD only focuses on the times the forecast predicted an event would occur. Thus, this measure is categorized as a discrimination statistic. POD is computed as

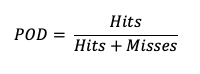
This measure is useful for rare events (tornadoes, 100-year floods, etc.) as it will penalize (i.e. go toward 0) the forecasts when there are too many missed forecasts. See how to use this statistic in METplus! 

Probability of False Detection (POFD)

A countermeasure to POD is the probability of false detection (POFD). POFD (also called false alarm rate), measures the frequency of false alarm forecasts relative to the frequency that an event does not occur.

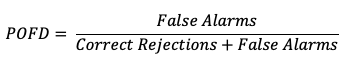
Together, POD and POFD measure forecasts’ ability to discriminate between occurrences and non-occurrences of the event of interest. See how to use this statistic in METplus!

Frequency bias (Bias)

Frequency bias (a measure of, you guessed it, bias!) compares the count of “yes” forecasts to the count of “yes” events observed.

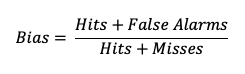
This ratio does not provide specific information about the performance of individual forecasts, but rather is a measure of over- or under-forecasting of the event. See how to use this statistic in METplus!

False Alarm Ratio (FAR)

The False Alarm Ratio (FAR) provides information about both the reliability and resolution attributes of forecasts. It computes the ratio of “yes” forecasts that did not occur to the total number of times a “yes” forecast was made (i.e., the proportion of “yes” forecasts that were incorrect).

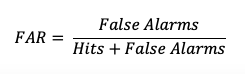
FAR also is the first statistic covered in this session that has a negative orientation: a FAR of 0 is desirable, while a FAR of 1 shows the worst possible ratio of “yes” forecasts that were not observed relative to total “yes” forecasts. See how to use this statistic in METplus! 

Critical Success Index (CSI)

The Critical Success Index (CSI), also commonly known as the Threat Score, is a second measure of the overall accuracy of forecasts (e.g., like the Accuracy measure mentioned earlier). Accuracy pertains to the agreement of individual forecast-observation pairs, and CSI can be calculated as

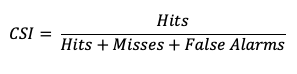
Note that by definition CSI can be described as the ratio between the times the forecast correctly called for an event and the total times the forecast called for an event or the event was observed. Thus, CSI ignores correct negatives, which differentiates it from percent correct. A CSI of 1 indicates a highly accurate forecast, while a value of 0 indicates no accuracy. See how to use this statistic in METplus!

Binary Categorical Skill Scores

Skill scores can be a more meaningful way of describing  a forecast’s quality. By definition, skill scores compare the performance of the forecasts to some standard or “reference forecast” (e.g., climatology, persistence, perfect forecasts, random forecasts). They often combine aspects of the previously-listed scalar statistics and can serve as a starting point for creating your own skill score that is better suited to your forecasts’ properties. Skill scores create a summary view of the contingency table, which is in contrast to the scalar statistics’ focus on one attribute at a time. 

Three of the most popular skill statistics for categorical variables are the Heidke Skill Score (HSS), the Hanssen-Kuipers Discriminant (HK), and the Gilbert Skill Score (GSS). These measures are described here.

Heidke Skill Score (HSS)

The HSS measures the proportion correct relative to the expected proportion correct that would be achieved by a “reference” forecast, denoted by C2 in the equation. In this instance, the reference forecast denotes a forecast that is completely independent of the observation dataset. In practice, the reference forecast often is based on a random, climatology, or persistence forecast. By combining the probability of a correct “yes” forecast (i.e., a hit) with the probability of a correct “no” forecast (i.e. a correct rejection) the resulting equation is

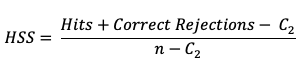
HSS can range from -1 to 1, with a perfect forecast receiving a score of 1. The equation presented above is a compact version which uses a sample climatology, C2 based on the counts in the contingency table. The C2 term expands to

This is a basic “traditional” version of HSS. METplus also calculates a modified HSS, that allows users to control how the C2 term is defined. This additional control allows users to apply an alternative standard of comparison, such as another forecast or a basic standard such as a persistence forecast or climatology. See how to use these skill scores in METplus!

Hanssen-Kuipers Discriminant (HK)

HK is known by several names, including the Peirce Skill Score and the True Skill Statistic. This score is similar to HSS (ranges from -1 to 1, perfect forecast is 1, etc.). HK is formulated relative to a random forecast that is constrained to be unbiased. In general, the focus of the HK is on how well the forecast discriminates between observed “yes” events and observed “no” events. The equation for HK is

which is equivalent to “POD minus POFD”. Because of its dependence on POD, HK can be similarly affected by infrequent events and is suggested as a more useful skill score for frequent events. See how to use this skill score in METplus!

Gilbert Skill Score (GSS)

Finally, GSS measures the correspondence between forecasted and observed “yes” events. Sometimes called the Equitable Threat Score (ETS), GSS is a good option for those forecasted events where the observed “yes” event is rare. In particular, the number of correct negatives (which for a rare event would be large) are not considered in the GSS equation and thus do not influence the GSS values. The GSS is given as

GSS ranges from -1 to 1, with a perfect forecast receiving a score of 1. Similar to HSS, a compact version of GSS is presented using the C1 term. This term expands to

 See how to use this skill score in METplus!

METplus solutions for Binary Categorical Forecast Verification

Now that you know a bit more about dichotomous, deterministic forecasts and how to extract information on the scalar attributes through statistics, it’s time to show how you can access those same statistics in METplus!

In order to better understand the delineation between METplus, MET, and METplus wrappers which are used frequently throughout this tutorial but are NOT interchangeable, the following definitions are provided for clarity:

• METplus is best visualized as an overarching framework with individual components. It encapsulates all of the repositories: MET, METplus wrappers, METdataio, METcalcpy, and METplotpy.
• MET serves as the core statistical component that ingests the provided fields and commands to compute user-requested statistics and diagnostics.
• METplus wrappers is a suite of Python wrappers that provide low-level automation of MET tools and plotting capability. While there are examples of calling METplus wrappers without any underlying MET usage, these are the exception rather than the rule.

MET solutions

The MET User’s Guide provides an Appendix that dives into all of the  statistical measure that MET calculates. METplus groups statistics together by application and type and makes them available to METplus users via several line types. For example, many of the statistics that were discussed above can be found in the Contingency Table Statistics (CTS) line type, which logically groups together statistics based directly on contingency table counts. In fact, MET allows users to directly access the contingency table counts through the aptly named Contingency Table Counts (CTC) line type.

The line types that are output by MET depend on your selection of the appropriate line type using the output_flag dictionary. Note that certain line types may or may not be available in every tool: for example, both Point-Stat and Grid-Stat produce CTS line types, which allow users to access the various contingency table statistics for both point-based observations and gridded observations. In contrast, Ensemble-Stat is the only tool that can generate a Ranked Probability Score (RPS) line type, which provides statistics relevant to the analysis of ensemble forecasts. If you don’t see your desired statistic in the line type or tool you’d expect it to be in, be sure to check the Appendix to see if the statistic is available in MET and which line type it’s currently grouped with.

As for the categorical statistics that were just discussed, here’s a link to the User’s Guide Appendix entry that discusses their use in MET:

• Accuracy
• POD
• POFD
• Bias
• FAR
• CSI
• HSS
• HSS_EC (HSS Expected Correct)
• HK
• GSS

Remember that for categorical statistics, including those that are associated with probabilistic datasets, you will need to provide an appropriate threshold that divides the observations and forecasts into two mutually exclusive categories. For more information on the available thresholding options, please review this section of the MET User’s Guide.

METplus Wrapper Solutions

The same statistics that are available in MET are also available with the METplus wrappers. To better understand how MET configuration options for the selection of statistics translate to METplus wrapper configuration options, you can utilize the Statistics and Diagnostics Section of the METplus wrappers User’s Guide, which lists all of the available statistics through the wrappers, including which tools can output particular statistics. To access the line types through the tool, select your desired tool and use this page to view a list of all available commands for that tool. Once you do, you’ll see that the tool will include several options that contain _OUTPUT_FLAG_. These options will exhibit the same behavior and accept the same settings as the line types in MET’s output_flag dictionary, so be sure to review the available settings to get the line type output you want.

The following two examples show a generalized method for calculating binary categorical statistics: one for a MET-only usage, and the same example but utilizing METplus wrappers. These examples are not meant to be completely reproducible by a user: no input data is provided, commands to run the various tools are not given, etc. Instead, they serve as a general guide of one possible setup among many that produce binary categorical statistics.

If you are interested in reproducible, step-by-step examples of running the various tools of METplus, you are strongly encouraged to review the METplus online tutorial that follows this statistical tutorial, where data is made available to reproduce the guided examples.

In order to better understand the delineation between METplus, MET, and METplus wrappers which are used frequently throughout this tutorial but are NOT interchangeable, the following definitions are provided for clarity:

• METplus is best visualized as an overarching framework with individual components. It encapsulates all of the repositories: MET, METplus wrappers, METdataio, METcalcpy, and METplotpy.
• MET serves as the core statistical component that ingests the provided fields and commands to compute user-requested statistics and diagnostics.
• METplus wrappers is a suite of Python wrappers that provide low-level automation of MET tools and plotting capability. While there are examples of calling METplus wrappers without any underlying MET usage, these are the exception rather than the rule.

MET Example of Binary Categorical Forecast Verification

This example demonstrates categorical forecast verification in MET.

For this example, let’s examine Grid-Stat. Assume we wanted to verify a binary temperature forecast of greater than 86 degrees Fahrenheit. Starting with the general Grid-Stat configuration file, the following would resemble the minimum necessary settings/changes for the fcst and obs dictionaries:

We can see that the forecast field name in the forecast input file is named TMP, and is set accordingly in the fcst dictionary. Similarly, the Z0 level is used to grab the lowest (0th) vertical level the TMP variable appears on. Finally, cat_thresh, which controls the categorical threshold that the contingency table will be created with, is set to greater than 86.0. This assumes that the temperature units in the file are in Fahrenheit. The obs dictionary is simply copying the settings from the fcst dictionary, which is a method that can be used if both the forecast and observation input files share the same variable structure (e.g. both inputs use the TMP variable name, in Fahrenheit, with the lowest vertical level being the desired verification level).

Now all that’s necessary would be to adjust the output_flag dictionary settings to have Grid-Stat print out the desired line types:

In this example, we have told MET to output the CTC and CTS line types, which will contain all of the scalar statistics that were discussed in this section. Running this set up would produce one .stat file with the two line types that were selected, CTC and CTS. The CTC line would look something like:

While the stat file full header column contents are discussed in the User’s Guide, the CTC line types are the final 6 columns of the line, beginning after the “CTC” column. The first value is MET’s TOTAL column which is the “total number of matched pairs”. You might better recognize this value as n, the summation of every cell in the contingency table. In fact, the following four columns of the CTC line type are synonymous with the contingency table terms, which have their corresponding MET terms provided in this table for your convenience:

Further descriptions of each of the CTC columns can be found in the MET User’s Guide. Note that the final column of the CTC line type, EC_VALUE, is only relevant to users verifying probabilistic data with the HSS_EC skill score.

The CTS line type is also present in the .stat file and is the second row. It has many more columns than the CTC line, where all of the scalar statistics and skill scores discussed previously are located. Focusing on the first few columns of the example output, you would find:

These columns can be understood by reviewing the MET User’s Guide guidance for CTS line type. After the familiar TOTAL or n column, we find statistics such as Base Rate, forecast mean, Accuracy, plus many more, all with their appropriate lower and upper confidence intervals and the bootstrap confidence intervals. Note that because the bootstrap library’s n_rep variable was kept at its default value of 0, bootstrap methods were not used and appear as NA in the stat file. While all of these statistics could be obtained from the CTC line type values with additional post-processing, the simplicity of having all of them already calculated and ready for additional group statistics or to advise forecast adjustments is one of the many advantages of using the METplus system.

METplus Wrapper Example of Binary Categorical Forecast Verification

To achieve the same outcome as the previous example but utilizing METplus wrappers instead of MET, very few changes would need to be made. Starting with the standard GridStat configuration file, we would need to set the _VAR1 settings appropriately:

Note how the BOTH option is utilized here (as opposed to individual FCST_ and OBS_ settings) since the forecast and observation datasets utilize the same name and level information. Because the loop/timing information is controlled inside the configuration file for METplus wrappers (as opposed to MET’s non-looping option), that information must also be set accordingly:

Finally, the desired line types need to be selected for output. In the wrappers, that looks like this:

After a successful run of METplus, the same .stat output file that was created in the MET example would be produced here, complete with CTC and CTS line type rows.